并查集学习笔记

发表于 更新于 分类于 ， 本文字数： 2.4k 阅读时长 ≈ 16 分钟
并查集学习时的一些笔记，主要为并查集的概念、模板以及应用场景。

定义

概念很重要，算法的核心就在于思想，而代码以及模板都是为了缩短解决问题的时间的手段，对于复杂问题来说，模板几乎没用。

言归正传，在计算机科学中，并查集是一种树型的数据结构，用于处理一些没有交集的集合（Disjoint Sets，一系列没有重复元素的集合）的合并及查询问题。对于每个集合，逻辑上都是一棵树，所有的操作都是基于树这个结构进行的。

并查集中主要有两种操作，即查询以及合并操作。

查询（Find）：给定一个节点x，找出该点的所在树的根节点root（注意不是x的父节点，查询操作主要用于判断两个节点x与y是否属于同一颗树上，所以只需要两个节点所在树的根节点就行）；也可以说是确定给定的元素属于哪一个子集。

合并（Union）：将两颗树合并为一棵树；也可以说将两个集合合并为一个集合。

代码模板及解释

此处的代码模板也只是适用于解决大多数问题的核心代码，理解核心代码，可以提高写并查集代码的速度。

初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int[] fa;// 节点对应索引值，fa[i]表示节点i的根节点
int[] rank;// 根节点为i的树的深度 作为优化的手段
/**
* 初始化
* @param n 节点的个数
*/
public void makeSet(int n) {
    fa = new int[n];
    rank = new int[n];
    Arrays.fill(rank,1);
    for(int i = 0; i < n; i++) {
        fa[i] = i;
    }
}

查询

原始版本

1
2
3
4
5
6
7
8
9
10
11
/**
* 查询指定节点的根节点
* @param x 节点
* @return 返回节点x的根节点
*/

public int find(int x) {
    // 如果根节点不是自己的 需要递归遍历得出自己的根节点
    if (fa[x] != x) 
        return find(fa[x]);
}

优化版本（称为“路径压缩”）

1
2
3
4
5
6
7
8
9
10
11
12
13
/**
* 查询指定节点的根节点
* @param x 节点
* @return 返回节点x的根节点
*/

public int find(int x) {
    // 如果根节点不是自己的 需要递归遍历得出自己的根节点
    if (fa[x] != x) {
        fa[x] = find(fa[x]);// 记忆化，直接更新x的根节点，使x成为fa[x]的孩子节点
    }
    return fa[x];
}

上述两种版本代码可以用一个树进行理解：

现有一颗树，树的节点为0，1，2，3，4，5，此时根节点为0，如图

图1 树

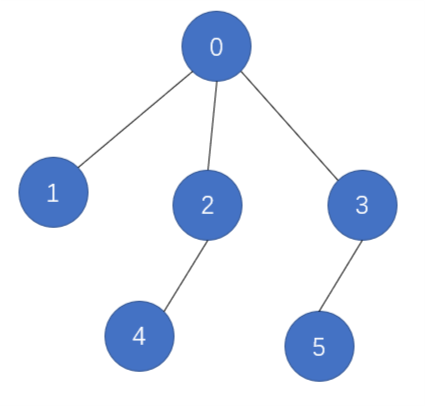
原始版本下查询后的结果如下：

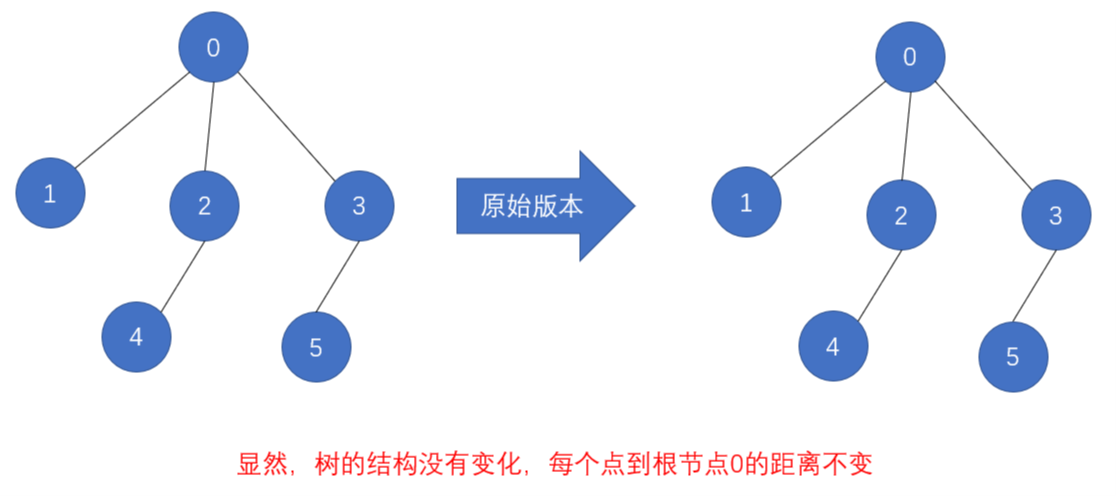
图2 查询-原始版本

优化版本下查询后的结果如下：

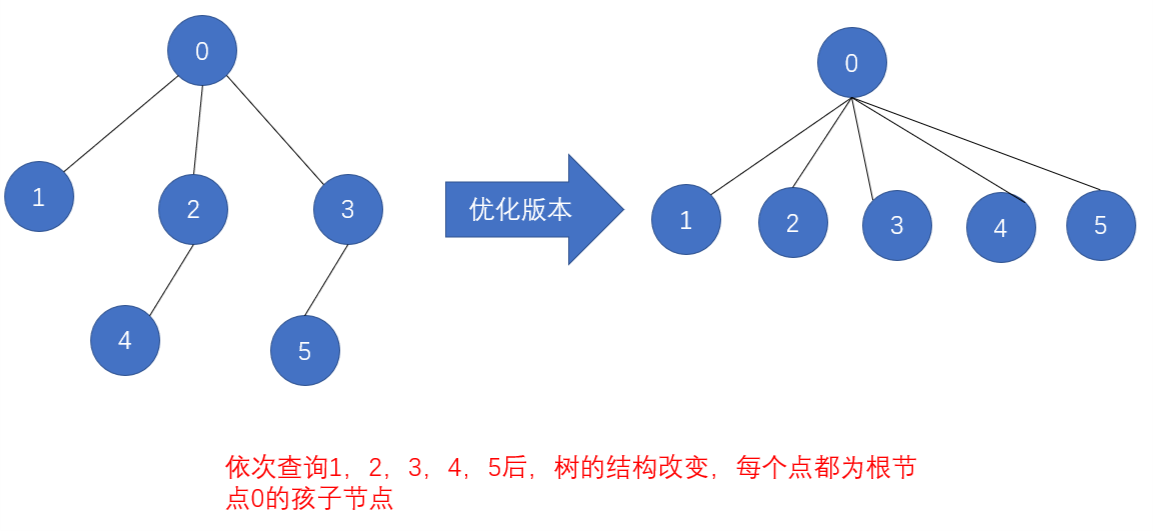
图3 查询-优化版本

从上述两图，就可以看出，优化版本会减少下一次查询同一个节点的根节点的递归深度，减少比较次数。

合并

原始版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
* 合并节点x对应的树与节点y对应的树
* @param x 节点x
* @param y 节点y
*/
public void union(int x,int y) {
    // 查找节点x的根节点
    int rootX = find(x);
    // 查找节点y的根节点
    int rootY = find(y);
    // 如果节点x与节点y的根节点一样 说明x与y在同一颗树上 不需要合并
    if (rootX == rootY) return;
    // 不同，则合并两棵树；即将一棵树的根节点作为另一颗树的孩子节点
    fa[rootY] = rootX;
}

优化版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
* 合并节点x对应的树与节点y对应的树
* @param x 节点x
* @param y 节点y
*/
public void union(int x,int y) {
    // 查找节点x的根节点
    int rootX = find(x);
    // 查找节点y的根节点
    int rootY = find(y);
    // 如果节点x与节点y的根节点一样 说明x与y在同一颗树上 不需要合并
    if (rootX == rootY) return;
    /*
    如果根节点不同，则要合并
    此时，将树的高度小的加到树的高度大的上面；如果高度一样的话，则随便，但合并后的树的高度要加一
    这样要注意一下：树的高度与find操作的时间复杂度的息息相关，find操作一次的时间复杂度为树的高度（最坏的情况下）
    */
    if (rank[rootX] < rank[rootY]) {
        // 将矮的树加到高的树上
        fa[rootX] = rootY;
    }
    // 树高一致
    else if (rank[rootX] == rank[rootY]) {
        fa[rootY] = rootX;
        rank[rootX]++;
    }
    else fa[rootY] = rootX;
}

再次举一个例子，就个图看会很容易理解，

现有两棵树：

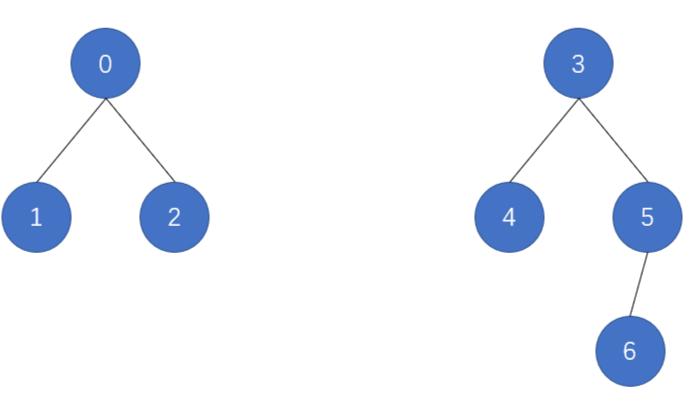
图4 两棵树

原始版本

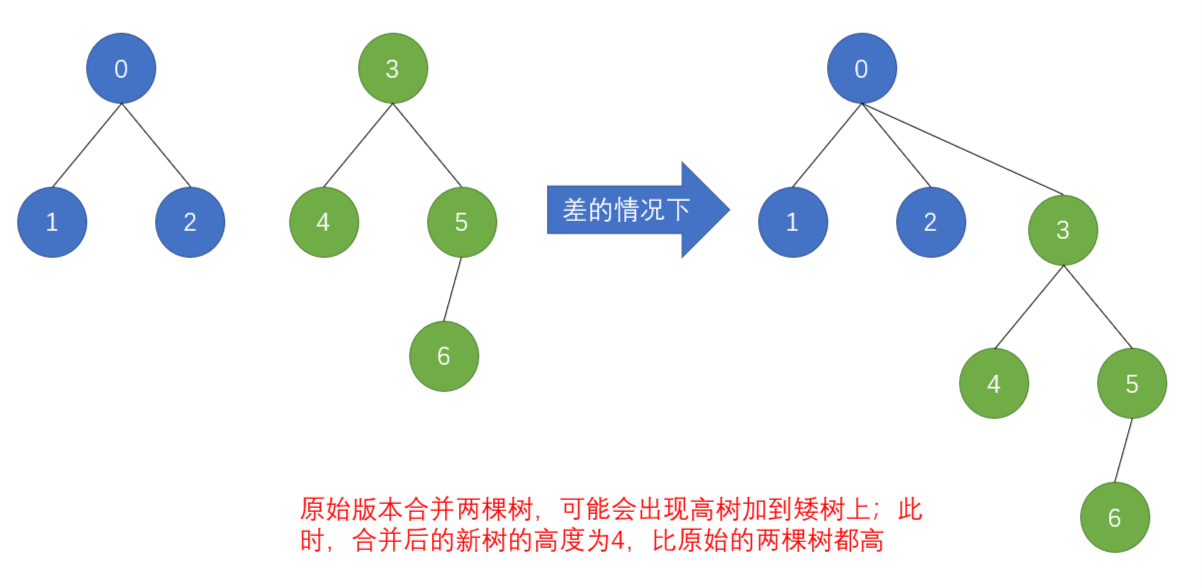
图5 合并-原始版本

优化版本

图6 合并-优化版本

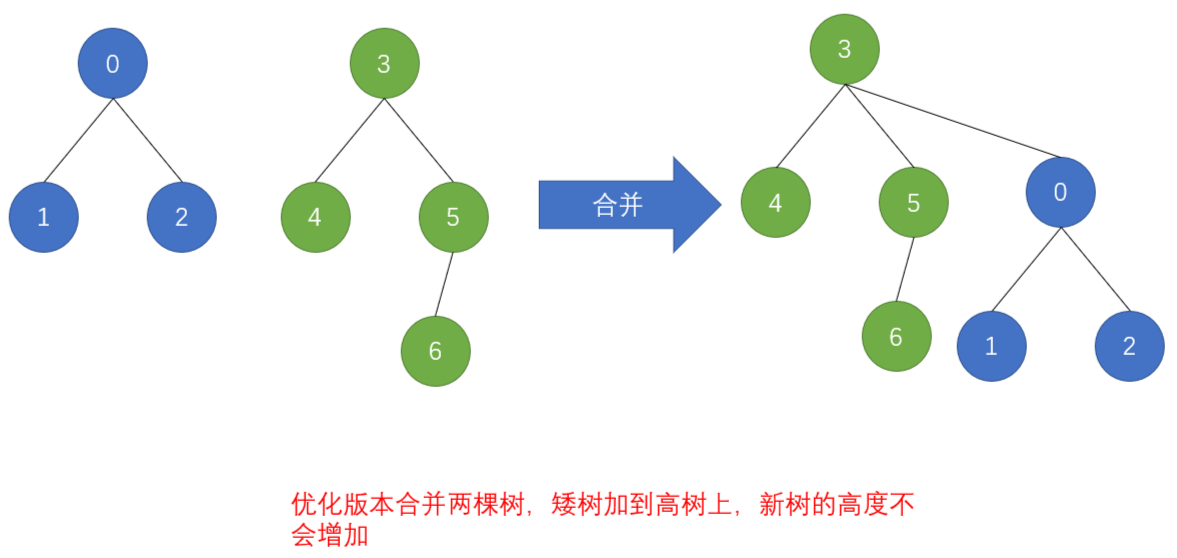
由上述两图可以看出，原始版本合并的新树的高度可能会增加，而优化版本的新树不会增加。树的高度直接影响之后的查询操作的时间复杂度。

应用场景

并查集可以解决的问题，一般DFS、BFS也可以解决，只不过时间复杂度高些。以下是可以使用并查集的场景：

  • 可以判断两个节点是否在同一个树中，也可以说判断两个节点是否在同一个连通子图中。（一个树也是一个连通图）
  • 统计极大连通子图的个数，即统计共有几个不同的根节点
  • 形成最小生成树（Kruskal算法）
  • 判断是否形成环，当两个节点的根节点都是同一个节点时，此时，形成了一个环

时间、空间复杂度

空间复杂度：因为要存储所有节点的索引，若节点数为n，则空间复杂度为O(n)

时间复杂度：这个没整明白O.O

趁热打铁

在力扣题库，按标签选择并查集，就可以看到所有并查集相关的题目了。

参考资料

维基百科：https://zh.wikipedia.org/wiki/%E5%B9%B6%E6%9F%A5%E9%9B%86

OI Wiki: https://oi-wiki.org/ds/dsu/v