题目链接
https://leetcode-cn.com/problems/01-matrix/
一波三折的解题
初看题目,这好像可以单源最短路径来解决。
初始思路
虽然一开始感觉可以用单源最短路径解决,但转念一想,好像并不需要这么麻烦,直接BFS解决也是可以的,就是找所有1到最近的0的距离么,BFS刚刚好。
设任意点的值为v,这个题目下的值只有0或1;任意点的距离值即答案为d;
然后整理下流程:
- 先找到01矩阵中v为1的点,将该点放入队列中。
- 然后从队列中拿出一个节点,用BFS的方式找出最近的一个v为0的点,并记录下距离d。
- 最后返回结果。
思路确实简单,而且也没啥毛病。但是我在BFS的时候用的是优先队列。事后我在想的时候,发现自己真是脑抽。但当时我是这样想的,对于当前的点,每一次把周围的四个点放到队列中,应该将距离值最小的点放到前面去,即优先弹出d小的点。其实,这是多此一举。因为先进入队列的都是d小的,后进入的肯定比前面进入的d至少多1。
此处还是贴上我心酸的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
|
public class Node implements Comparable<Node>{
private int x;
private int y;
private int val;
public Node(int x, int y) {
this.x = x;
this.y = y;
val = 0;
}
public int getX() {
return x;
}
public void setX(int x) {
this.x = x;
}
public int getY() {
return y;
}
public void setY(int y) {
this.y = y;
}
public int getVal() {
return val;
}
public void setVal(int val) {
this.val = val;
}
@Override
public int compareTo(Node o) {
return this.val - o.getVal();
}
}
public class Solution {
public int[][] updateMatrix(int[][] matrix) {
int row = matrix.length;
int column = matrix[0].length;
int[][] ans = new int[row][column];
Queue<Node> queue = new LinkedList<>();
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
if (matrix[i][j] == 1) queue.add(new Node(i,j));
}
}
while (!queue.isEmpty()) {
bfs(queue.remove(),ans,matrix,row,column);
}
return ans;
}
private void bfs(Node start, int[][] ans,int[][] matrix, int row,int column) {
boolean[][] visit = new boolean[row][column];
PriorityQueue<Node> queue = new PriorityQueue<>();
visit[start.getX()][start.getY()] = true;
queue.add(start);
int[][] directions = {{0,-1},{-1,0},{0,1},{1,0}};
int nextX,nextY;
while (!queue.isEmpty()) {
Node cur = queue.remove();
if (matrix[cur.getX()][cur.getY()] == 0) {
ans[start.getX()][start.getY()] = cur.getVal();
return;
}
for (int i = 0; i < 4; i++) {
nextX = cur.getX()+directions[i][0];
nextY = cur.getY()+directions[i][1];
if (nextX >= 0 && nextX < row && nextY >= 0 && nextY < column && !visit[nextX][nextY]) {
visit[nextX][nextY] = true;
Node nextNode = new Node(nextX,nextY);
nextNode.setVal(cur.getVal()+1);
queue.add(nextNode);
}
}
}
}
}
|
结果:提交后超时。我想原因应该是优先队列的多此一举和重复遍历。
其中重复遍历是这个意思:
对于已知道距离d2的点m,如果当时的点为n,距离值为d1,BFS后遇到了m,将m放进队列时给这个点的距离值设置为d1+1。但m点是已知距离值的,即d1+d2这个距离就可以遇到一个v=0的点,这个d1+d2是可以利用的,这个值可能就是答案,也可能不是。
举个例子:
如这样的01矩阵: 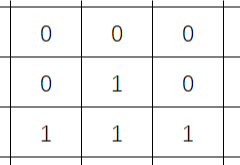
当程序进行到这里的时候: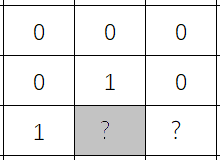
此时,队列弹出的点是图2中的灰色框,那么按照BFS遍历,这个点的下一层为下图所示:
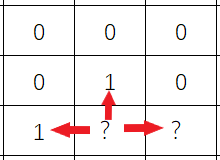 图3
图3
可以发现,进入队列中的有三个点,但是其中2个点都是有值,按照一般流程会在进行下一层的遍历,这样其实会浪费一些时间,而我们可以利用两个已知值的点省略掉一些遍历。
对于已知距离值d的点,我们在进行BFS遍历到该点时就可以不需要在遍历该店的周围的点,如果遍历了,那就是重复遍历。
最终的思路
经过一番脑细胞死亡的过程,我想到最终AC的思路。
简而言之,就是用已知距离值的点推出未知距离值的点.
流程如下:
- 队列首先压入v=0且d=0的点,这些点就是初始时v=0的点。我们可以将这些点称为第一层的点。
- 之后,弹出上一层的每一个点,并对每个点进行BFS遍历,如果遍历到v=1的点且之前没有遍历过,计算距离值d,压入队列,这些点记为第二层的店。可以确定的是,对于每个遍历到的v=1的点x,其d的值都是最优的值(这个用反证法就很容易证明出来)。第二层的点的d都为1.
- 之后,重复2步骤,直到队列中没有节点。返回结果。
贴上代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| public class Solution {
public int[][] updateMatrix(int[][] matrix) {
int row = matrix.length;
int column = matrix[0].length;
int[][] ans = new int[row][column];
boolean[][] visit = new boolean[row][column];
Queue<Node> queue = new LinkedList<>();
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
if (matrix[i][j] == 0) {
queue.add(new Node(i,j));
visit[i][j] = true;
}
}
}
int[][] directions = {{0,-1},{-1,0},{0,1},{1,0}};
int nextX,nextY;
while (!queue.isEmpty()) {
Node cur = queue.remove();
for (int i = 0; i < 4; i++) {
nextX = cur.getX()+directions[i][0];
nextY = cur.getY()+directions[i][1];
if (nextX >= 0 && nextX < row && nextY >= 0 && nextY < column && !visit[nextX][nextY]) {
visit[nextX][nextY] = true;
Node nextNode = new Node(nextX,nextY);
ans[nextX][nextY] = cur.getVal()+1;
queue.add(nextNode);
}
}
}
return ans;
}
}
public class Node {
private int x;
private int y;
public Node(int x, int y) {
this.x = x;
this.y = y;
}
public int getX() {
return x;
}
public void setX(int x) {
this.x = x;
}
public int getY() {
return y;
}
public void setY(int y) {
this.y = y;
}
}
|


